W fizyce, wektor to niezwykle ważna wielkość, która łączy w sobie zarówno wartość liczbową, jak i kierunek oraz zwrot. W przeciwieństwie do skalarnych wielkości, takich jak temperatura czy masa, wektory dostarczają nam informacji o tym, jak coś się przemieszcza lub jaką siłę wywiera. Przykłady wektorów obejmują siłę, prędkość oraz przemieszczenie, które są kluczowe w zrozumieniu ruchu ciał w przestrzeni.
Wektory są reprezentowane graficznie jako strzałki, gdzie długość strzałki odpowiada wartości wektora, a kierunek wskazuje, w którą stronę działa ta wielkość. Zrozumienie wektorów jest fundamentalne dla wielu dziedzin fizyki, ponieważ pozwala na precyzyjne opisywanie i analizowanie ruchów oraz sił. W tym artykule przyjrzymy się bliżej, czym są wektory, jakie mają właściwości oraz jak można je stosować w praktyce.
Kluczowe informacje:- Wektor to wielkość fizyczna z wartością, kierunkiem i zwrotem.
- Przykłady wektorów to siła, prędkość i przemieszczenie.
- Wektory można dodawać, odejmować i mnożyć przez skalar.
- Wektor przemieszczenia łączy punkt początkowy z końcowym w ruchu ciała.
- W przeciwieństwie do skalara, wektor uwzględnia zarówno odległość, jak i kierunek.
Definicja wektora w fizyce i jego podstawowe cechy
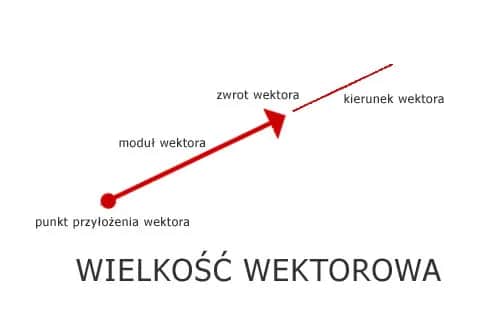
W fizyce, wektor to wielkość, która łączy w sobie wartość liczbową, kierunek oraz zwrot. To właśnie te trzy cechy sprawiają, że wektory są tak istotne w analizie ruchu i sił. Przykłady wektorów obejmują siłę, prędkość oraz przemieszczenie. Każdy z tych wektorów jest reprezentowany graficznie jako strzałka, gdzie długość strzałki odpowiada wartości wektora, a kierunek wskazuje, w którą stronę działa ta wielkość.
Wartość wektora informuje nas o jego mocy lub prędkości, natomiast kierunek i zwrot pokazują, jak i w którą stronę ta wielkość działa. Dzięki temu, wektory odgrywają kluczową rolę w wielu dziedzinach fizyki, od mechaniki po dynamikę. Zrozumienie wektorów pozwala na lepsze analizowanie zjawisk fizycznych i ułatwia obliczenia związane z ruchem ciał.
Jakie są kluczowe właściwości wektora w fizyce?
Kluczowe właściwości wektora to jego moduł, kierunek oraz zwrot. Moduł to długość strzałki, która wskazuje wartość wektora. Kierunek to kąt, pod jakim wektor jest skierowany w przestrzeni, natomiast zwrot określa, w którą stronę wektor działa. Te właściwości są niezbędne do zrozumienia, jak wektory współdziałają w różnych sytuacjach fizycznych.
Przykłady wektorów w fizyce, które ułatwiają zrozumienie
W świecie fizyki, wektory mają kluczowe znaczenie, a ich zrozumienie jest niezbędne do analizy ruchu i sił. Przykłady wektorów, takie jak siła i prędkość, pokazują, jak te wielkości wpływają na obiekty w ruchu. Siła, na przykład, jest wektorem, który wskazuje zarówno intensywność, jak i kierunek działania. W praktyce oznacza to, że siła działająca na obiekt może zmieniać jego prędkość lub kierunek ruchu.
Wektor prędkości z kolei informuje nas o tym, jak szybko i w którą stronę porusza się obiekt. Na przykład, samochód jadący z prędkością 60 km/h na północ ma określoną prędkość, która jest wektorem. Dzięki tym przykładom, łatwiej jest zrozumieć, jak wektory w fizyce są stosowane do opisu ruchu i interakcji między obiektami.
Jak siła i prędkość są reprezentowane jako wektory?
Siła i prędkość są reprezentowane graficznie jako strzałki. Długość strzałki wskazuje ich wartość, a kierunek pokazuje, w którą stronę działają. Na przykład, siła 10 N skierowana na wschód będzie miała strzałkę o długości proporcjonalnej do 10 N, wskazującą na wschód. Prędkość również jest reprezentowana w ten sam sposób, co ułatwia wizualizację ruchu obiektów.
- Przemieszczenie – zmiana położenia obiektu w określonym kierunku.
- Prędkość – szybkość ruchu w określonym kierunku.
- Siła – działanie wpływające na ruch obiektu w określonym kierunku.
- Przyspieszenie – zmiana prędkości obiektu w czasie.
Czytaj więcej: Jak skutecznie przygotować się do matury rozszerzonej z fizyki i uniknąć błędów
Operacje na wektorach: co musisz wiedzieć, aby je zrozumieć
Operacje na wektorach są kluczowe dla ich zrozumienia i zastosowania w fizyce. Możemy dodawać, odejmować oraz mnożyć wektory przez skalar. Dodawanie wektorów polega na łączeniu ich wartości i kierunków. Na przykład, jeśli mamy dwa wektory: jeden o wartości 5 N na północ i drugi o wartości 3 N na wschód, ich suma będzie nowym wektorem, który wskazuje w kierunku północno-wschodnim.
Odejmowanie wektorów działa na podobnej zasadzie, ale polega na odwróceniu kierunku jednego z wektorów przed dodaniem. Mnożenie wektora przez skalar zmienia jego długość, ale nie kierunek. Na przykład, jeśli pomnożymy wektor siły 10 N przez 2, otrzymamy nowy wektor o wartości 20 N w tym samym kierunku. Zrozumienie tych operacji jest niezbędne dla analizy ruchu i sił w fizyce.
Jak dodawać i odejmować wektory w praktyce?
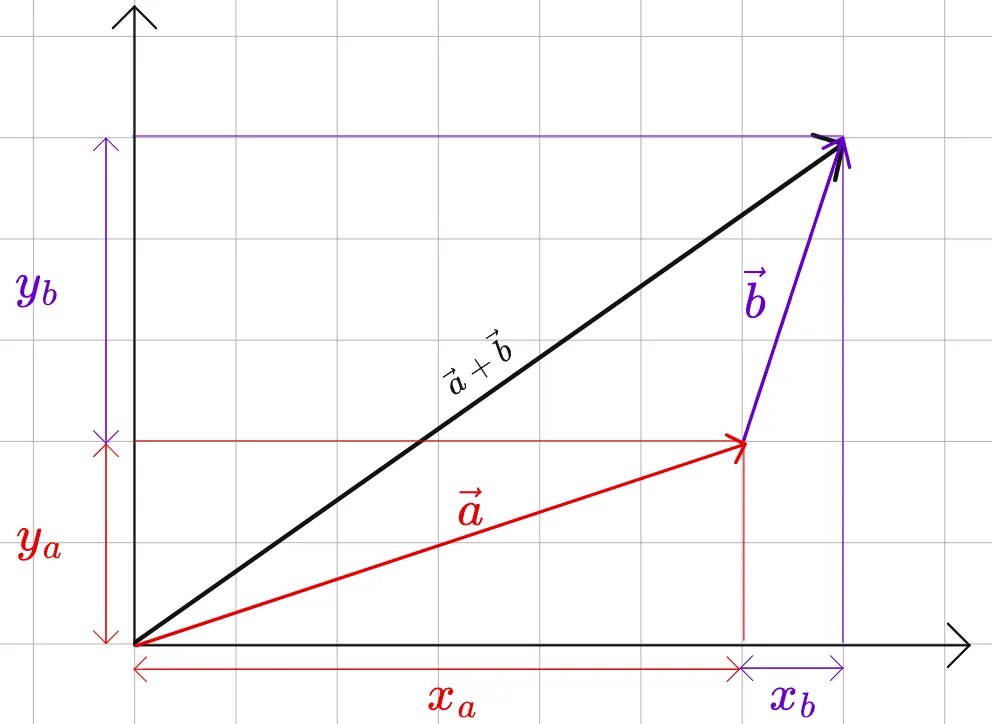
Dodawanie i odejmowanie wektorów to kluczowe operacje w analizie zjawisk fizycznych. Można to zrobić na dwa główne sposoby: metodą głowy do ogona oraz metodą równoległoboku. W metodzie głowy do ogona, końcówka jednego wektora jest łączona z początkiem drugiego wektora, a nowy wektor jest tworzony od początku pierwszego wektora do końca drugiego. Z kolei metoda równoległoboku polega na rysowaniu równoległoboku, gdzie dwa wektory są bokami, a przekątna tego równoległoboku reprezentuje ich sumę.
Odejmowanie wektorów polega na dodaniu wektora o przeciwnym kierunku. Na przykład, aby odjąć wektor A od wektora B, dodajemy wektor -A do wektora B. To podejście jest niezwykle przydatne w praktycznych zastosowaniach fizycznych, gdzie często musimy zrozumieć, jak różne siły wpływają na obiekt.
| Metoda | Opis |
| Głowa do ogona | Łączenie końca jednego wektora z początkiem drugiego. |
| Równoległobok | Tworzenie równoległoboku z dwóch wektorów, przekątna reprezentuje sumę. |
Wektory a skalary: kluczowe różnice, które warto znać
Wektory i skalary różnią się fundamentalnie w fizyce. Wektory mają zarówno wartość, jak i kierunek, podczas gdy skalary mają tylko wartość. Na przykład, temperatura jest skalarem, ponieważ określa tylko ilość ciepła, nie wskazując kierunku. Z drugiej strony, prędkość jest wektorem, ponieważ mówi nie tylko, jak szybko coś się porusza, ale również w którą stronę.
Dlaczego porównanie wektorów i skalarów jest istotne?
Zrozumienie różnicy między wektorami a skalarami jest kluczowe dla analizy i interpretacji zjawisk fizycznych. Wiele problemów fizycznych wymaga uwzględnienia zarówno wektorów, jak i skalarów, aby uzyskać pełny obraz sytuacji. Na przykład, w przypadku ruchu samochodu, ważne jest nie tylko, jak szybko się porusza (prędkość), ale również w którą stronę (kierunek). To zrozumienie pomaga w podejmowaniu właściwych decyzji w kontekście ruchu i sił.
Wizualizacja wektorów: jak diagramy pomagają w nauce
Wizualizacja wektorów jest niezwykle ważna w nauce, ponieważ pomaga w zrozumieniu ich właściwości i działań. Diagramy pozwalają zobaczyć, jak wektory współdziałają ze sobą w przestrzeni. Używanie graficznych reprezentacji, takich jak strzałki, sprawia, że złożone koncepcje stają się bardziej przystępne i zrozumiałe.
Jak graficznie przedstawiać wektory i ich operacje?
Graficzne przedstawianie wektorów można zrealizować na kilka sposobów. Najpopularniejsze metody to metoda głowy do ogona oraz metoda równoległoboku, które wcześniej omówiliśmy. Rysowanie wektorów na płaszczyźnie, z odpowiednimi długościami i kierunkami, ułatwia zrozumienie, jak różne siły wpływają na ruch obiektów. Dzięki wizualizacji, studenci i naukowcy mogą szybciej analizować i interpretować dane fizyczne.
Wektory w fizyce: kluczowe różnice i ich zastosowanie w analizie
W artykule omówiono, jak wektory różnią się od skalarów oraz jakie mają fundamentalne znaczenie w zrozumieniu zjawisk fizycznych. Wektory, które posiadają zarówno wartość, jak i kierunek, są niezbędne do analizy ruchu i sił, co ilustrują przykłady takie jak prędkość i siła. W przeciwieństwie do nich, skalary, takie jak temperatura, mają tylko wartość, co ogranicza ich zastosowanie w kontekście dynamiki.
W artykule podkreślono również znaczenie wizualizacji wektorów w nauce, która ułatwia zrozumienie ich właściwości i operacji. Metody takie jak głowa do ogona oraz równoległobok pozwalają graficznie przedstawiać wektory, co czyni złożone koncepcje bardziej przystępnymi. Dzięki tym technikom, zarówno studenci, jak i profesjonaliści mogą efektywniej analizować i interpretować dane fizyczne, co jest kluczowe dla skutecznej nauki i zastosowania w praktyce.