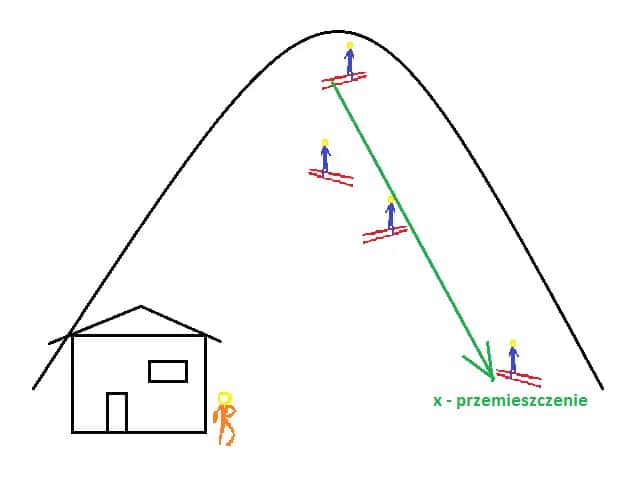
Przemieszczenie w fizyce to kluczowe pojęcie, które odgrywa fundamentalną rolę w analizie ruchu ciał. Definiowane jako wektor łączący położenie początkowe z położeniem końcowym, przemieszczenie informuje nas o tym, jak daleko i w jakim kierunku ciało się przemieściło. W przeciwieństwie do drogi, która mierzy całkowitą długość toru, przemieszczenie uwzględnia jedynie najkrótszą odległość między dwoma punktami, co czyni je istotnym narzędziem w kinematyce. Wartość przemieszczenia może być dodatnia, ujemna lub równa zero, co wskazuje na kierunek ruchu względem osi układu współrzędnych.
W artykule omówimy znaczenie przemieszczenia w kontekście ruchu prostoliniowego i krzywoliniowego, a także jego wpływ na obliczanie prędkości i przyspieszenia. Zrozumienie tego pojęcia jest kluczowe nie tylko w teorii, ale także w praktycznych zastosowaniach, które napotykamy na co dzień. Przedstawimy również przykłady przemieszczenia w codziennym życiu, aby zobrazować, jak ta koncepcja wpływa na nasze zrozumienie ruchu.
Kluczowe wnioski:
- Przemieszczenie jest wektorem, który łączy położenie początkowe i końcowe ciała.
- Wartość przemieszczenia może być dodatnia, ujemna lub równa zero, w zależności od kierunku ruchu.
- Przemieszczenie różni się od drogi, która jest wielkością skalarną i zawsze dodatnia.
- Obliczanie prędkości i przyspieszenia opiera się na wartościach przemieszczenia.
- Przemieszczenie jest kluczowe w analizie ruchu prostoliniowego i krzywoliniowego.
- Przykłady przemieszczenia w codziennym życiu pomagają lepiej zrozumieć tę koncepcję.
Definicja przemieszczenia w fizyce i jego podstawowe cechy
Przemieszczenie w fizyce to wektor, który łączy położenie początkowe z położeniem końcowym ciała w ruchu. Informuje nas o tym, jak daleko i w jakim kierunku ciało się przemieściło. Jest to fundamentalne pojęcie w kinematyce, które opisuje zmianę położenia ciała w przestrzeni. Wartość przemieszczenia jest zawsze mniejsza lub równa drodze pokonanej przez ciało, ponieważ przemieszczenie mierzy najkrótszą odległość między dwoma punktami, niezależnie od rzeczywistej trasy.
Przemieszczenie ma zarówno kierunek, jak i wartość, co oznacza, że jest wielkością wektorową. Jego wartość wyraża się w jednostkach długości, takich jak metry. Wartość wektora przemieszczenia jest zawsze dodatnia i mówi o odległości, podczas gdy znak współrzędnej wektora wskazuje kierunek przemieszczenia względem wybranego układu współrzędnych. Przemieszczenie może być dodatnie, ujemne lub równe zero, w zależności od kierunku ruchu względem osi. Na przykład, jeśli ciało wróci do punktu początkowego, jego całkowite przemieszczenie wynosi zero, nawet jeśli przebyło znaczną drogę.
Wektor przemieszczenia: co to oznacza i jak go mierzyć
Wektor przemieszczenia jest kluczowym elementem w analizie ruchu. Mierzy on zmianę położenia ciała, a jego wielkość i kierunek są istotne dla zrozumienia ruchu. Aby go zmierzyć, należy znać współrzędne początkowe i końcowe. W ruchu prostoliniowym przemieszczenie można obliczyć jako różnicę współrzędnych końcowej i początkowej. W przypadku ruchu krzywoliniowego wymagane są bardziej złożone metody analizy, takie jak obliczenia wektorowe.
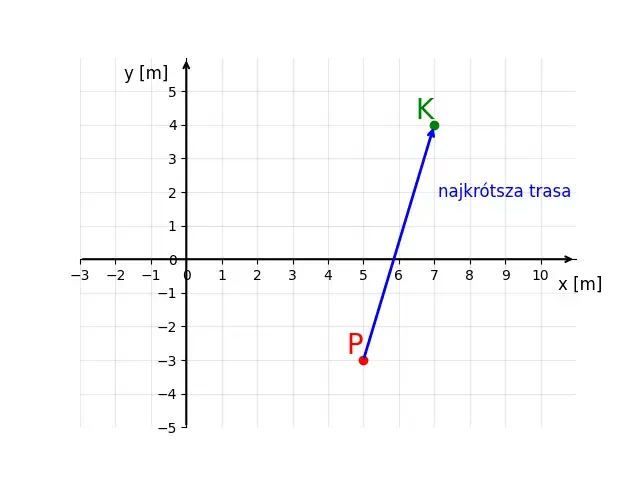
- Wektor przemieszczenia można reprezentować graficznie jako strzałkę, gdzie długość strzałki odpowiada wartości przemieszczenia, a kierunek wskazuje kierunek ruchu.
- Przemieszczenie można obliczyć, korzystając z formuły: Δx = x2 - x1, gdzie x2 to położenie końcowe, a x1 to położenie początkowe.
- Wartość przemieszczenia jest istotna w kontekście analizy ruchu, ponieważ pozwala na obliczanie prędkości i przyspieszenia ciała.
Różnice między przemieszczeniem a drogą: kluczowe aspekty
Przemieszczenie i droga to dwa różne pojęcia w fizyce, które często są mylone. Przemieszczenie to wektor, który łączy położenie początkowe z położeniem końcowym, wskazując zarówno odległość, jak i kierunek. Z kolei droga to wartość skalarna, która mierzy całkowitą długość toru, bez względu na kierunek ruchu. Wartość przemieszczenia może być mniejsza, równa lub większa od drogi, w zależności od trasy, jaką przebyło ciało. Na przykład, jeśli ktoś przemieszcza się w kółko, jego droga może być znaczna, ale przemieszczenie wyniesie zero, ponieważ wraca do punktu początkowego.
- Przemieszczenie jest wektorem, który ma kierunek i wartość, podczas gdy droga jest wartością skalarną, zawsze dodatnią.
- W przypadku prostoliniowego ruchu, przemieszczenie można łatwo obliczyć jako różnicę współrzędnych końcowych i początkowych, a droga to całkowita długość przebytej trasy.
- Przykład: Jeśli samochód przejedzie 100 km w jedną stronę i następnie wróci do punktu startowego, jego przemieszczenie wyniesie 0 km, podczas gdy droga to 200 km.
Znaczenie przemieszczenia w analizie ruchu ciał
Przemieszczenie odgrywa kluczową rolę w analizie ruchu ciał, ponieważ pozwala na dokładne określenie zmiany położenia. Dzięki temu, możemy zrozumieć, jak szybko i w jakim kierunku porusza się obiekt. Obliczanie prędkości opiera się na wartościach przemieszczenia, co czyni je niezbędnym elementem w kinematyce. Przemieszczenie jest również podstawą do określenia przyspieszenia, które z kolei informuje nas o tym, jak zmienia się prędkość obiektu w czasie.
Wartość przemieszczenia jest zawsze mniejsza lub równa drodze pokonanej przez ciało, co podkreśla jego znaczenie w analizie ruchu. W praktyce, znajomość przemieszczenia umożliwia naukowcom i inżynierom modelowanie i przewidywanie ruchu obiektów w różnych warunkach. W ten sposób przemieszczenie staje się kluczowym narzędziem w badaniach i zastosowaniach inżynieryjnych, gdzie precyzyjne obliczenia są niezbędne do osiągnięcia zamierzonych rezultatów.
Jak przemieszczenie wpływa na obliczanie prędkości i przyspieszenia
Przemieszczenie jest fundamentalnym elementem w obliczaniu prędkości i przyspieszenia. Prędkość oblicza się, dzieląc przemieszczenie przez czas, w którym to przemieszczenie miało miejsce. Wzór na prędkość to: v = Δx / Δt, gdzie Δx to przemieszczenie, a Δt to czas. Przyspieszenie natomiast definiuje się jako zmianę prędkości w czasie, co również jest ściśle związane z przemieszczeniem. Wzór na przyspieszenie to: a = Δv / Δt, gdzie Δv to zmiana prędkości.
| Scenariusz | Przemieszczenie (m) | Prędkość (m/s) | Przyspieszenie (m/s²) |
| Ruch prostoliniowy | 100 | 10 | 2 |
| Ruch krzywoliniowy | 50 | 5 | 1 |
Przemieszczenie w kontekście ruchu prostoliniowego i krzywoliniowego
Analiza przemieszczenia w ruchu prostoliniowym i krzywoliniowym różni się znacznie, co wpływa na metody obliczeń. W ruchu prostoliniowym przemieszczenie można łatwo obliczyć jako różnicę między współrzędnymi końcowymi a początkowymi, co oznacza, że stosuje się prostą formułę: Δx = x2 - x1. Z kolei w ruchu krzywoliniowym, gdzie trajektoria jest zakrzywiona, obliczenia stają się bardziej złożone. W takim przypadku konieczne jest uwzględnienie kształtu toru, co często wymaga zastosowania metod wektorowych i analizy kątów.
W ruchu krzywoliniowym przemieszczenie można obliczyć, dzieląc tor na mniejsze odcinki i stosując odpowiednie metody geometryczne. Na przykład, w przypadku ruchu po okręgu, przemieszczenie jest określane na podstawie kąta obrotu oraz promienia okręgu. Różnice w obliczeniach przemieszczenia między tymi dwoma typami ruchu są kluczowe dla zrozumienia dynamiki obiektów i ich zachowania w różnych warunkach.
Czytaj więcej: Co oznacza rw w fizyce? Zrozumienie jednostek pracy i mocy
Przykłady przemieszczenia w fizyce: praktyczne zastosowania
Przemieszczenie można zaobserwować w wielu codziennych sytuacjach, co pozwala lepiej zrozumieć jego znaczenie. Na przykład, gdy ktoś idzie do sklepu oddalonego o 300 metrów, jego przemieszczenie wynosi 300 metrów w kierunku sklepu, niezależnie od tego, jaką trasą się poruszał. Jeśli ta osoba wróci do punktu wyjścia, całkowite przemieszczenie wyniesie 0 metrów, mimo że przebyła 600 metrów. Innym przykładem może być rowerzysta, który jedzie wzdłuż parku, pokonując krętą trasę; jego przemieszczenie będzie określone przez najkrótszą odległość między punktem startowym a końcowym, a nie przez długość toru, który pokonał.
Kolejnym przykładem jest samochód, który jedzie z jednego miasta do drugiego. Jeśli jego położenie początkowe to Warszawa, a końcowe to Kraków, przemieszczenie wyniesie około 300 kilometrów w kierunku południowym. Jednakże, jeśli samochód zjeżdża z trasy i pokonuje dodatkowe 50 kilometrów, jego droga wzrośnie, ale przemieszczenie pozostanie takie samo, ponieważ odnosi się do odległości między dwoma punktami. Te przykłady pokazują, jak przemieszczenie odzwierciedla najkrótszą trasę między dwoma położeniami, co jest kluczowe w analizie ruchu.
Przemieszczenie w codziennym życiu: zrozumienie przez przykłady
W codziennym życiu przemieszczenie można zauważyć na wiele sposobów. Na przykład, gdy dziecko bawi się w parku, a następnie wraca do domu, jego przemieszczenie wyniesie zero, jeśli wróci do punktu startowego, mimo że spędziło dużo czasu na zabawie. Innym przykładem jest osoba, która przemieszcza się z jednego końca pomieszczenia do drugiego. Jeżeli przeszła 5 metrów w prawo, a następnie 5 metrów w lewo, jej całkowite przemieszczenie również wyniesie zero, mimo że przebyła 10 metrów. Te sytuacje pomagają zrozumieć, jak przemieszczenie działa w praktyce i jak różni się od drogi.
Jak przemieszczenie wpływa na technologie i inżynierię przyszłości
W miarę jak technologia rozwija się, przemieszczenie odgrywa coraz większą rolę w innowacyjnych rozwiązaniach inżynieryjnych i technologicznych. Na przykład, w dziedzinie robotyki i autonomicznych pojazdów, precyzyjne obliczanie przemieszczenia jest kluczowe dla nawigacji i planowania tras. Dzięki zastosowaniu zaawansowanych systemów GPS oraz czujników, roboty i pojazdy mogą dokładnie określać swoje położenie i dostosowywać trasę w czasie rzeczywistym, co zwiększa efektywność i bezpieczeństwo.
W przyszłości, z wykorzystaniem sztucznej inteligencji, możliwe będzie jeszcze dokładniejsze modelowanie ruchu, co pozwoli na lepsze prognozowanie i optymalizację tras w transporcie publicznym i dostawach. Analiza danych związanych z przemieszczeniem może również przyczynić się do rozwoju inteligentnych miast, gdzie zarządzanie ruchem i planowanie przestrzenne będą oparte na rzeczywistych wzorcach przemieszczenia mieszkańców. Tego rodzaju innowacje mogą znacząco wpłynąć na jakość życia w miastach, zmniejszając zatory komunikacyjne i poprawiając dostępność usług.